Variational Bayesian approximation¶
Minimizing Kullback-Leibler divergence¶
- lower bound
Mean-field, fixed form¶
Variational Bayesian expectation maximization algorithm¶
(conjugate exponential family models)
Todo
Split and fix the text below into the sections
In variational Bayesian (VB) methods, the idea is to find an approximate distribution \(q(Z)\) which is close to the true posterior distribution \(p(Z|Y)\) (see, e.g., [13][1][4][6]). The dissimilarity is defined as the Kullback-Leibler (KL) divergence of \(p(Z|Y)\) from \(q(Z)\):
The divergence is always nonnegative and zero only when \(q(Z)=p(Z|Y)\). However, the divergence cannot typically be evaluated because the true posterior distribution is intractable.
The key idea in VB is that the divergence can be minimized indirectly by maximizing another function which is tractable. This function is a lower bound of the log marginal likelihood. It can be found by decomposing the log marginal likelihood as
Because the KL divergence is always non-negative, \(\mathcal{L}(q)\) is a lower bound for \(\log p(Y)\). Furthermore, because the sum of \(\mathcal{L}(q)\) and \(\mathrm{KL}(q \| p)\) is constant with respect to \(q\), maximizing \(\mathcal{L}( q)\) is equivalent to minimizing \(\mathrm{KL}(q \| p)\). In some cases, even \(\mathcal{L}(q)\) may be intractable and further approximations are needed to find a tractable lower bound.
Thus far, there is nothing approximate in the procedure, because the optimal solution which minimizes the divergence is the true posterior distribution \(q(Z) = p(Z|Y)\). In order to find a tractable solution, the range of functions needs to be restricted in some way. However, the range must be as rich and flexible as possible in order to find as good an approximation as possible. This can be achieved by assuming a fixed functional or factorial form for the distribution.
This work restricts the class of approximate distributions by assuming that the \(q\) distribution factorizes with respect to some grouping of the variables:
where \(Z_1,\ldots,Z_M\) form a partition of \(Z\). The notation is kept less cluttered by ignoring the subscript on \(q\). The lower bound \(\mathcal{L}(q)\) can be maximized with respect to one factor at a time. The optimal factor \(q(Z_m)\) can be found by inserting the approximate distribution eqref{eq:VB_factorized} to \(\mathcal{L}(q)\) and maximizing \(\mathcal{L}(q)\) with respect to \(q(Z_m)\). This yields
where the expectation is taken over all the other factors except \(q(Z_m)\). An iterative update of the factors until convergence is called the variational Bayesian expectation maximization (VB-EM) algorithm ([1][3]). Alternatively, it is also possible to use, for instance, gradient-based optimization methods to optimize the parameters of the approximate \(q\) distributions (see, e.g., [11] or stochastic variational inference ([10]) in order to improve scaling to large datasets with stochastic optimization.
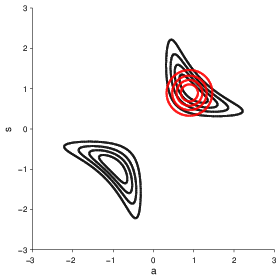
Figure 1: An illustration of typical effects of the factorizing approximation. A true posterior (in black) and the optimal factorizing VB posterior (in red).
Fig. 1 illustrates typical effects of the factorizing VB approximation: only one mode of the true posterior is captured, dependencies between variables are lost and marginal distributions are too narrow.